In the formalism of Quantum Mechanics the wavelike aspect of fundamental particles, and aggregate matter, has been an integral feature, ever since Louis de Broglie presented his ground breaking thesis in 1923.⁵ However, no explanation has ever been presented as to what a matter wave is, or consists of, in the sense of 'what' is 'waving'. They are not defined in the ontology of QM, beyond Born's rule of determining a particle's probable location from the square of the wavefunction's amplitude. While their reality as physical entities is not assumed, they nonetheless form the foundation of the famous Schrödinger wave equation, and consequently the basis of all chemistry at the atomic and molecular scale. A largely heuristic concept is presented here that exploits symmetry principles to try to resolve this curious ambiguity.

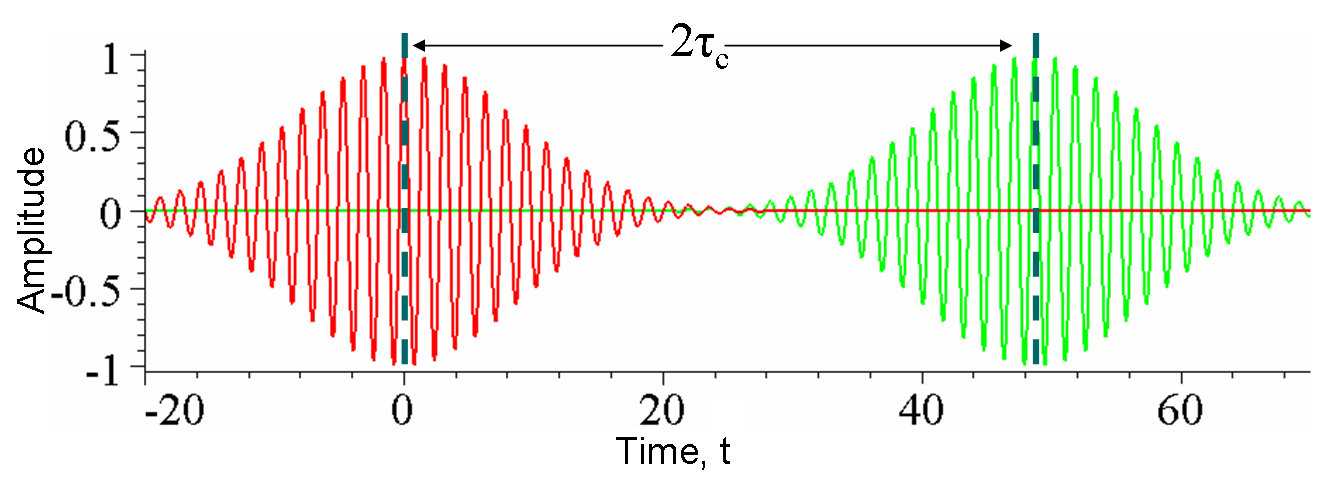
Consider a duality, between the exceedingly weak gravitational field and 10³⁹ times stronger electromagnetism, entailing a transposition of the variables of the respective fields - a process technically known as an S-Duality.⁷ How would you accomplish this? First consider that gravity, a tensor field, is measured by a particular amount of length contraction, and a proportional degree of time dilation, at each point in space. In turn, electromagnetism, a vector field, has a particular magnitude and direction of the electric and magnetic components at each point in space. [Caveat: See Electroweak and Higg's at end of this article.]

Since each of these fields possesses a pair of variables, to implement the duality, one simply swaps variable-pairs between the fields. That generates two new fields - a tensor field with electric and magnetic parameters, and a vector field with length and time variables. To a sentient being, residing in a parallel brane-universe, having an electric-magnetic continuum, and composed of matter that incorporates this field swap, all the laws of physics, from his perspective, would be identical to ours. Implicit in the behavior of this alternate brane-universe is that the electric-magnetic tensor field acquires the precise properties of the gravitational field in our universe, while the length-time vector field acts exactly like the electromagnetic field in our universe.

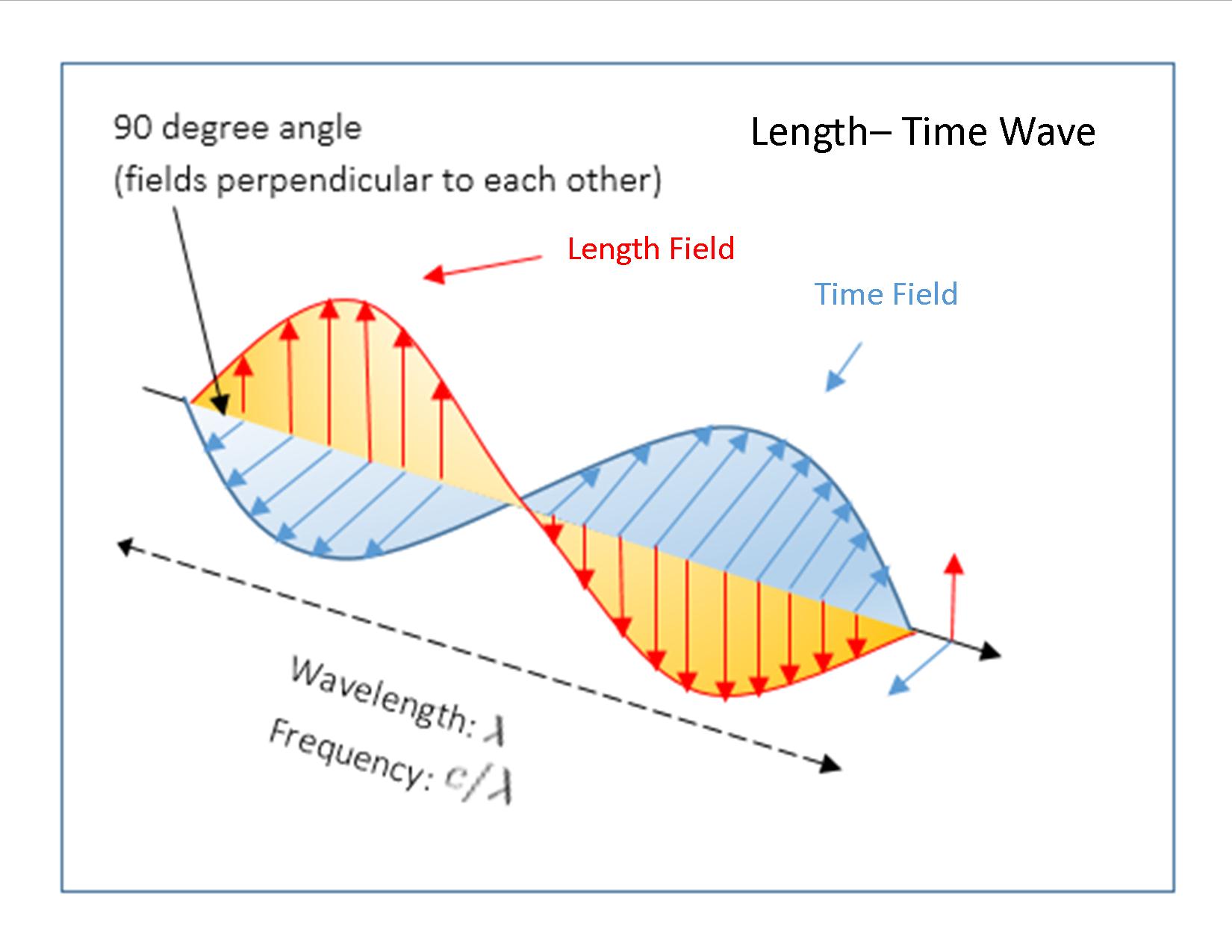
Next suppose this putative length-time vector field (with intrinsic strength matching the electromagnetic field) is actually present in our universe. It's automatically ruled out at the macroscale, as it would conflict with known physics. But it could be hiding at the microscale, assuming it acquires a sufficiently large mass in our universe that has not yet been probed by the LHC. How would such a field manifest, aside from revealing its massive quanta: a length-time 'photon'? Possible answer: It may already be an integral part of our physics - in the form of matter waves. [As a historical footnote, Erwin Schrödinger once entertained the notion that matter waves represented a real disturbance in space, analogous to the field variables in electromagnetic waves.³]

Neglecting, (for the moment), this putative field's microscopic range (r<10^-19 m.), imagine a length-time wave propagating through our universe. Due to the postulated S-duality it is structurally identical to an electromagnetic wave; except that the electric and magnetic components are replaced by length and time components. In an electromagnetic wave the electric and magnetic fields are mutually perpendicular to one another, and to the direction of the wave's propagation. The electric field oscillates between negative and positive potentials, while the magnetic field oscillates between north and south polarities.

How would one define the analogous excursions, of the length and time components, in a propagating length-time wave? The answer is straightforward. When the wave is in the 'positive' portion of its cycle physical lengths are positive and time flows in the forward direction. When the wave goes into the 'negative' portion of its cycle physical lengths are negative and time flows in the reverse direction. Since we posit that the wave occupies three dimensional space, this means that during the 'positive' excursions the volume enclosed by the wave occupies the kind of space we associate with a positive matter/energy universe (ours). Conversely, during the 'negative' excursions it occupies the space we associate with a negative matter/energy universe - e.g. a universe with an inverted 4D coordinate system - negative height, length, width, and reversal of the direction of time. As explained at this link, (Dual Universe), such a negative-energy universe could explain the 120 magnitude discrepancy between the calculated quantum vacuum energy in our universe, and its observed value. It could also explain the origin of dark energy.

At first glance one might expect a length-time wave to have energy associated with it, just like an electromagnetic wave. However, from the preceding arguments it follows that a length-time wave oscillates between negative and positive energy states of the vacuum, but averages out to zero energy, assuming equal magnitude departures in the opposing energy states. Thus a length-time wave has zero net energy. This accords with Louis de Broglie's assertion, in his 1923 Comptes Rendus note,⁵ that matter waves, of themselves, cannot involve the transport of energy from place to place. [See reference 14.]

Now imagine an observer entrained at the positive-to-negative crossover point of this, (temporarily macroscopic), length-time wave. He would see spacetime behind him expanding, and characterized by a positive energy state of the vacuum. Towards his front he sees spacetime contracting, and characterized by a negative energy state of the vacuum. This, essentially, is the metric signature of an Alcubierre warp ⁴ (below). Now replace the observer with a fundamental particle - an electron - and restore the length-time field's microscopic range: (presumed to be less than 10^-19 m.), to see how this might potentially work in nature.

The Alcubierre metric neutralizes large external acceleration forces on an object within its flat space region. The, (now vanishingly small), cross-over node of the length-time wave would effectively be such a region, as the length and time variables are unchanging at this point on the wave. Since this length-time field is imbued with the same strength as the electromagnetic field (via the S-Duality mechanism), enormous tidal forces, (severe spacetime curvatures), would be created within its confined range (or warp bubble). These tidal forces should be sufficient to counteract the enormous 10²² g's angular accelerations, typically experienced by an electron orbiting a nucleus.¹⁰ This would explain the absence of synchrotron radiation in atomic structures, if we assume stable electrons are locked, on average, at the cross-over point of the length-time wave (a.k.a. matter wave).

By specifying "on average" the supposition is that the quantum vacuum, in proximity to fundamental particles, is populated by numerous length-time 'photons', whose mean wavelength corresponds to the particle's de Broglie wavelength. Collectively, these 'photons' would thus form the equivalent of a "wave packet", which would modulate the behavior of the particle as perceived by external observers. In essence what would otherwise be classical trajectories for fundamental particles, would be radically modified by a particle's wave packet - consisting of a cloud of length-time quanta in the particle's immediate neighborhood. Being that these length-time 'photons', are assumed to possess a mass in the supersymmetry regime, the range of their length and time wave components would be restricted to less than 10^-19 meters. This would explain the spatial confinement of the wavepacket¹¹, associated with fundamental particles, as it evolves in time. Alternatively, essentially the same result would be obtained by assuming fundamental particles are not perfectly 'locked' at the cross-over node, but oscillate symmetrically to either side of it. That would dispense with the need for a 'packet' of length-time quanta in a particle's vicinity.

It is sometimes stated in popular expositions on quantum physics that the absence of synchrotron radiation in atomic structures is due to electrons forming "stationary states", and thus it is not necessary to invoke the classical concept of an actual orbiting electron. The idea is that since electrons are smeared out in a symmetrical cloud about the nucleus, they are not actually undergoing physical movement, as in a classical picture. In reality, every electron in an atom has a particular quantized angular momentum L associated with it, indicating orbital motion is actually occurring even if the electron itself is non-localized, appearing only as a symmetrical charge distribution about the nucleus. As will be explained below, this 'smearing out' of electrons into symmetrical clouds, would result from variations in the amplitude and 'polarity' of the length and time components of the length-time field.

A key implication of this idea is that during the positive, or expansion phase, of these metric fluctuations, the spacetime curvature would clearly be positive, so that there would be a mismatch between the externally measured volume and the warp bubble's internal volume (similar to Van den Broek's variant of the Alcubierre metric⁶). During the contraction phase spacetime curvature would go negative, and the volume containing the particle would expand to the same degree, but into the negative spatial regime. This all may sound strange, but spacetime can expand or contract at any rate, as far as is currently known. These volumetric changes would be quite extreme due to the intrinsic strength of this postulated field. They would also be extraordinarily rapid, as an electron in the lowest orbital of the hydrogen atom completes 6.6 x 10¹⁵ orbital cycles per second.

These extreme volumetric oscillations within a tiny (<10^-19 m.) region surrounding fundamental particles should equate to a cyclical motion of regression and advancement relative to external reference frames; e.g. other particles (observers). This cyclical change in effective distance between fundamental particles, would, in turn, lead to a de-synchronization of clocks, or sync shifts (relativity of simultaneity); part of the suite of Lorentzian transformations. These sync shifts would be hugely magnified due to the large, and rapid, variations in volume within the warp bubbles enveloping every fundamental particle, and translate to forward and backward oscillations in time, which, nonetheless, average to the present moment, locally.

Richard Feynman once observed that a positron (positive electron) could be thought of as an ordinary electron moving backwards in time. Since 50% of the time a length-time quanta mediated temporal wave is flowing backwards in time, an electron under its influence should appear more positive in charge during that interval. Conversely, the forward sweep in time for the other 50% of a length-time wave cycle should lead to enhancement of the electron's negative charge, so that, overall, the electron's charge magnitude is conserved.

These temporal-induced oscillations in the electron's charge, above and below its actual value, should influence the orbital behavior of an electron, and thus the shape of the orbit. The depiction of the s, p, d, f electron orbits (below), derived from various combinations of the three quantum numbers (n, l, and m), plugged into the Schrödinger equation, show spherical, lobe-like, and donut-shaped regions of varying densities. This visual representation of solutions to the Schrödinger wave equation illustrates the probability that the electron will, at times, be found quite close to the nucleus, and at other times quite far from the nucleus.

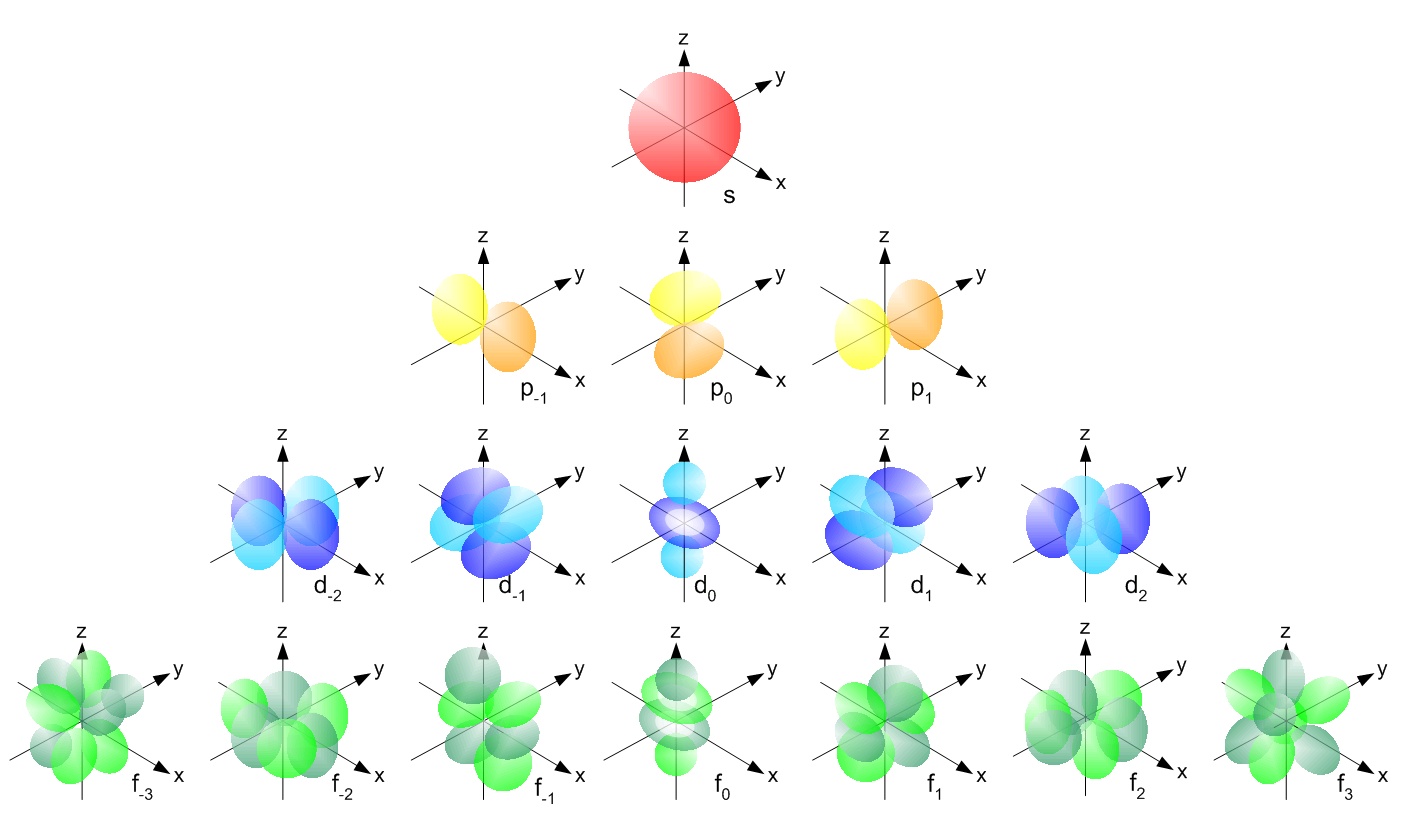
Logically, it would make sense that during the negative charge enhancement portion of the length-time wave (a.k.a. matter wave), the electron will be found closer to the nucleus, while during the diminishment of the electron's negativity (trending more positive) it will be found further from the nucleus. Naturally, the average distance of the electron to the nucleus would be determined by the average magnitude of the electron's charge, throughout its orbit, which would correspond to its measured value. It may also be possible that these temporally-induced variations in the electron's charge, above and below its measured value, contributes, somewhat, to interatomic bonding, as a result of a region of an electron cloud in one atom, being more electro-positive, attracting an enhanced electro-negative region in another atom's electron cloud.

The influence of the length-time (hereafter L-T for brevity) field on fundamental particles would result in a particle being distributed symmetrically throughout both time (past and future) and space (positive and negative), as it is acted on by the ensemble of L-T waves (quanta) in its vicinity. This L-T field induced 'smearing' of a fundamental particle's location in time and space suggests what the "collapse of the wavefunction" might actually entail, particularly in conjunction with John Cramer's Transactional Hypothesis detailed below. If we imagine a floating soap bubble as a particle's overall energy dispersed through space (positive and negative), and time (past and future), this would correspond to the particle's pre-collapse wavefunction. The 'popping' of that bubble then corresponds to the collapse of that particle's wavefunciton, as all the energy of the bubble dispersed throughout a large region of space and time collapses into a single locale and time.

The forward/backward translations in time, induced in every particle by the oscillating L-T waves, dovetails perfectly with John Cramer's Transactional Interpretation of quantum mechanics, by providing an underlying mechanism for such temporal oscillations. In addition, the excursions into negative energy states of the vacuum would provide the natural medium to generate the "advanced" (backwards-in-time) electromagnetic waves essential to the theory. Taking his cue from the Wheeler-Feynman Absorber theory, Cramer recognized that the fully relativised version of Schrödinger's wave equation described the evolution of a quantum system not only into the future, but into the past as well. The implication was that the Absorber theory, originally applied to light, might be extended to particles as well, since in quantum theory particles are treated as wave packets.

Schrödinger's wave equation represents the potential of a quantum system before it collapses into some, unspecified, future state. The equation is in the form of a complex function containing both real and imaginary parts, and has two sets of solutions. The first solution set is the one utilized by most physicists to calculate quantum processes, and describes the evolution of a quantum system into the future. The second set of equations, known as the complex conjugate, is a mirror image of the first, and describes the evolution of a quantum system into the past.

In Cramer's Transactional Interpretation every quantum event represents a "handshake" across spacetime. An "offer" wave from an excited electron propagates outward in an ever expanding bubble, corresponding to the first Schrödinger wave equation. At some future time the energy of this expanding wavefront is randomly absorbed by a second electron, (or other charged particle), which then transmits a "confirmation" wave back into the past towards the original excited electron, arriving at the exact instant that electron radiated its initial signal. This confirmation wave, which travels into the past, corresponds to the complex conjugate of the first wave equation. Additionally, the original excited electron also sends a confirmation wave into the past, while the absorber electron sends an offer wave into the future. These two cancel out, however, while the primary confirmation wave, possessing negative energy, reinforces the primary offer wave, and the transaction is complete.

The hydrogen atom is the simplest atomic system, with a single electron orbiting a proton. From the foregoing considerations, in order for the electron and proton, pirouetting about their common center of mass, to stay bound, their respective L-T waves, (matter waves), would have to be in phase, (on average), with each other. If their respective matter waves were persistently out of phase, the hydrogen atom would become unstable due to a mismatch in the electric charge magnitude the electron and proton present to each other. Additionally, their local 'clocks', (mediated by the T component of the L-T field modulating each particle), would be out of sync. They thus would not be exactly opposite and equal in charge magnitude (overall average integrated through time). If, for example, the electron were ensconced somewhere within the negative-energy portion of the L-T wave, it would diminish its negative charge, and increase its average distance from the nucleus.

At first glance it would not seem possible for the electron and proton de Broglie wavelengths to match as the proton is 1836 times the mass of the electron. For a fundamental particle: λ = h/p, where λ is the wavelength associated with a particle, p is the particles momentum, and h is Planck's constant. However, p, which is momentum, is the product of mass x velocity. Since the electron and proton are moving around their combined system center-of-mass, and that center is close to, or inside, the proton, there is a reciprocal trade-off. The mass of the proton is much larger than the electron's but its mean velocity is proportionally smaller, so their de Broglie wavelengths are the same.

With both the electron and proton L-T waves being in phase with each other, their respective Alcubierre micro-warps would be in sync with one another, and both particles would be embraced within inertial, non-accelerated frames. Not feeling acceleration, within their micro-warps, neither particle would radiate synchrotron radiation, despite observers in an external frame perceiving the particles to be undergoing angular acceleration. With that in mind, the known participation of nucleons in the phenomena of super-conductivity (isotope effect) makes perfect sense. The hydrogen atom system could be considered a limited case of 'superconductivity' wherein the electron and proton 'currents', confined to closed-loop paths, would exhibit zero 'resistance', as no energy would be dissipated in the form of synchrotron radiation. Large scale superconductivity could then be conceived as a choreographed 'dance' between proton-pairs, (in separate atoms), synchronously linked to a particular Cooper electron pair. As Cooper-pairs migrate through the material, they might trade off their original synchronous proton-pair with another proton-pair.

In actual Type-1 superconductivity the BCS theory perfectly describes the processes going on inside the superconducting material. When the materials critical temperature is reached, electrons condense into Cooper pairs, with opposing spin, thus jointly behaving like a single Bosonic entity. Additionally, these correlated electrons experience a net attraction in the milli-electron volt range, induced by interaction with lattice phonons, or quantized lattice vibrations. But it could be that the time reverse mechanism with attendant polarity reversal, described above, is what actually is responsible for this attraction. The Cooper pair electrons would not have to be fully 180 degrees temporally out of phase, as that would lead to a net attraction equal to that between an electron and proton, but only slightly out of phase to achieve the predicted milli-electron volt attraction between members of a Cooper pair.

In 1990 Tate et. al.⁹ found a disagreement between the theoretically predicted value of the Cooper-pair mass in a spinning niobium superconductor, and its experimentally determined value. Intrigued by this finding a group of researchers at the Austrian Research Center (ARC) subjected ring shaped, niobium superconductors to rapid angular accelerations in a liquid helium bath.⁸ They detected anomalously large ( up to 277 micro-g) acceleration signals as the ring shaped superconductors were spun-up about their central axes.

The ARC group interpreted this acceleration signal (which opposed the applied acceleration) to be a gravitoelectric field, induced by a time-varying gravitomagnetic field. When the ARC team attempted to detect the gravitomagnetic field directly with sensitive gyroscopes, they found only 1% of the signal they were expecting. Furthermore, this supposed gravitomagnetic field did not follow the inverse square rule as was expected. Additionally, a follow-up experiment by a group in New Zealand, using a ring laser gyroscope to detect a gravitomagnetic field from a spinning lead superconductor failed to detect any gravitomagnetic field. ¹²

The proposed L-T field could explain the acceleration signals detected in the radial, (and off radial), plane of the niobium superconductor, (around its entire circumference), during spin-up. Since the L-T field reacts to and opposes acceleration forces until equilibrium is restored, an acceleration signal opposite to the direction of the niobium rings angular acceleration makes sense. As no force operates instantaneously the 10^-5 g acceleration signals detected, during the niobium superconductor's spin-up (and spin-down), would have arisen from a lag in the L-T field's response time, even though the maximum tangential acceleration at the outer rim of the ring was only 7.33 g's.

Assuming the L-T field is not able to compensate instantly, in real time, for the acceleration force applied to both the lattice sites and Cooper-pair electrons, it may be that a small, momentary 'leakage' of negative-energy gravitons (from a higher dimensional bulk space) is projected along the axes of acceleration. Since positive-energy gravitons mediate an attractive force, (in the quantized version of gravity), negative-energy gravitons would be expected to mediate a repulsive force. But for spins to balance in this reaction, an equal quantity of positive-energy gravitons would need also to be emitted in the opposite direction (for their force effect to be additive).

What's particularly intriguing is that the controversial Evgeny Podkletnov¹³ claimed a similar effect when he subjected a Yittrium-Barium-Copper-Oxide (YBCO) superconductor to 2 million volt discharges. Comparing Podkletnov's experiment with the ARC group's experiment is, admittedly, like comparing apples with oranges. The one feature they do have in common is that they both accelerate cooper-pairs and lattice sites (in Podkletnov's case the lattice site protons would be slightly displaced for the brief interval of 10^-4 sec., before rebounding to their original position, or perhaps returning to their equilibrium position after a damped oscillation). The ARC experimenters apply 7.33 g's in the same direction for both the cooper-pairs and lattice sites yielding 100 micro-g's signal. Podkletnov's experiment discharges 2 million volts between a YBCO superconductor and a copper plate, in a partially evacuated chamber, yielding a claimed1000 g's for 10^-4 sec.

Electrons, in a vacuum, subjected to such a voltage will reach about 98% c. Assuming this occurs in the 100 micro-second interval, indicated in Dr. Giovanni Modanese's paper, the average acceleration on the electrons is something like 10⁹ g's. Curiously, if one substitutes the proton's mass, in place of the electron's, the resulting acceleration is only 7.3% below a perfect linear extrapolation of the ARC team's applied acceleration versus signal yield. That is pretty remarkable, since this near perfect linearity is maintained across eight orders of magnitude. Also, since the proton has the opposite charge of the electron the acceleration pulse (on the protons) would be opposite in direction to the detected signal; as was the case in the ARC experiments.

It might be assumed that the greater the acceleration experienced by a superconductor, the higher the frequency of positive and negative energy gravitons emitted, just as the more rapid acceleration, or de-acceleration, of an electron will result in emission of higher frequency electromagnetic waves. This, however, is something of a guess, since this is uncharted territory, and the exact relationship between the frequency of these putative gravitons and the applied acceleration is unknown. In any case, the protons (lattice sites) in Podkletnov's superconductor would have been subjected to about a million times the acceleration as the protons in the ARC group's superconductor, presumably resulting in the brief emission of much higher frequency positive and negative energy gravitons. This may account for the narrow, collimated beam effect reported by Podkletnov, versus an apparent widely dispersed 'spray' of gravitons in the ARC team's experiment, necessary to explain the off-axis acceleration signals detected. This would be perfectly analogous to intermediate frequency radio waves (kilohertz range, say), whose energy cannot be focused in a narrow beam because of the long wavelengths.

As intimated earlier a duality between gravity and the electromagnetic field constitutes an incomplete picture, and thus represents only an approximation. Instead, it's proposed that the electromagnetic-gravity duality is embraced within a larger duality between the electroweak force and gravity-Higg's (where General Relativistic gravity combines with the Higg's field). That leaves only one other force - the Strong force, for a total of three forces, at some energy above the electroweak synthesis. By the permutation rule N!, where N=3, there are six possible permutations or dualities between three elements. These six resulting, novel rearrangements of nature's fields are proposed to correspond to the six sub-theories of M-Theory, which themselves are related to one another by various dualities. This concept is discussed in more detail here: M-Theory